Contents
ABSTRACT
Scientometrics indicators vary widely across subareas of the Computer Science (CS) discipline. Most researchers have previously analyzed scientometrics data specific to a particular subfield or a few subfields. More popular subareas lead to high scientometrics, and others have lower values. This work considers seven diversified CS subareas and six commonly used scientometrics indicators. First, we study the varying range of chosen scientometrics indicators of various subareas of the CS discipline. We explore the correlation patterns of these six indicators. Then, we consider a few combinations of these indicators and apply K-means clustering to decompose the pattern space. Correlation findings indicate that though the highly correlated indicators vary for most subfields, no single indicator can be considered equally suitable for all the subareas. The K-means clustering results show distinctive patterns across subfields, which are stable across K. The clustered subfield-specific indicators are quite distinct across subfields. This knowledge can be used as a signature for partitioning the subarea-specific indicators.
INTRODUCTION
Publication venues are considered an essential component of the scientific community for disseminating research findings: discovery and facts. The tremendous growth of scientific literature and publication venues poses a severe challenge in assessing its credibility. Publishing research in high-impact journals is often symbolized as a sign of prestige and a measure of the quality of research. For this, the scientific publications are evaluated by several Scientometrics Indicators (SIs). The ranking of publications is also utilized in various decisions, such as hiring, career promotion, tenure, funding, awards, etc. Thus, various scientometrics studies have been devoted to analyzing the prominence of publication venues and collecting the relevant information of publication data from multiple disciplines.[1,2]
Due to emerging growth in scientific publications, it is not trivially accessible for researchers to find suitable and credible venues for their publication. Moreover, numerous quantitative indicators have also been proposed for assessing the publication data; such indicators are increasing, and there are conflicting opinions at times. Yet, such well-defined indicators provide valuable information to a researcher and are used for the research evaluation process. Despite several usages, their face value may not be used without understanding their interpretation.
Generally, it is believed that the higher value of such indicators represents a high impact. However, this is not true for several cases. For example, the h-index of the last year’s Nobel Prize winner (2022) in Theoretical Physics, Prof. John F. Clauser, is 29 (Source: Google Scholar), which is relatively low compared to high achievers. Though such a low number is justified in the area of Theoretical Physics, this may not be the case with other high achievers in other subareas of Physics. Thus, the study of subarea-specific indicators of a major area/discipline is paramount. In this work, we have considered Computer Science (CS) discipline and its subareas. There are some studies done by researchers in several major disciplines. In the domain of CS, previous studies have used some subareas of Computer Science.[3–5]
Moreover, various scientometrics indicators are proposed by researchers for assessing the impact of publications. In the main, Impact Factor is the most used scientometrics indicator.[6,7] Different publication houses or database holders also developed other emerging metrics, such as CiteScore, SJR, SNIP, h5-index, etc.[8–12] By utilizing such indicators, researchers have studied correlation analysis and assessed the impact of CS research publications.
In the CS discipline, for example, Serenko[3] has ranked journals of Artificial Intelligence based on citation-based indices and concluded that ranking based on selected metrics correlated perfectly with one another and strongly correlated with the journal’s Impact Factor. On the contrary, Tsai[4] considered five subareas of CS, namely, Artificial Intelligence (AI), Information Systems (IS), Software Engineering (SE), Theory and Methods (TM), and Interdisciplinary Applications (IA). The author found a low correlation between the Impact Factor and h-index for these five subareas. Other researchers have also compared AI journals’ survey-based and citation-based rankings and concluded that such rankings should be complementary.[5] In addition, several other researchers have utilized soft computing techniques for bibliometric studies.[2,13-15] Moreover, journal rankings vary across indicators and databases.[16] Another study concluded that a single scientometrics metric might not be suitable for evaluation.[17]
We argue the scientometrics indicators vary widely across the disciplines and their subareas. Highly impactful and prestigious journals of some subareas of CS, such as Theoretical CS (TCS), get a lower rank/value. Furthermore, due to the highly diverse nature of Computer Science’s discipline and its subareas, publication practices and their readerships differ significantly. Some studies have inferred the use of multiple indicators or combinations to quantify the publications instead of a single indicator.[17,18] A few studies have combined indicators in their research to assess the journal publications of CS.[3,4,19] However, to our knowledge, no research has been devoted to quantitatively analyzing the varying scientometric indicators across CS subareas.
In this work, we select seven diversified and major CS subareas, namely, Artificial Intelligence/Machine Learning (AI/ML), Computer Graphics (CG), Computer Networks and Wireless Communication (CNWC), Computer Vision and Pattern Recognition (CVPR), Database and Information Systems (DBIS), Software Systems (SS), and Theoretical Computer Science (TCS), as included in Table 1. These subareas have been selected from the Google Scholar database, wherein we picked the publication venues/journals from the Top 20. This research is specific to the CS discipline, though similar studies could be done to any subject/discipline of Arts, Sciences, Social Sciences, Engineering, etc.
| Abbreviations | for | Type |
|---|---|---|
| AI/ML | Artificial Intelligence/Machine Learning. | Subarea 1 |
| CG | Computer Graphics. | Subarea2 |
| CNWC | Computer Networks and Wireless Communication. | Subarea3 |
| CVPR | Computer Vision and Pattern Recognition. | Subarea4 |
| DBIS | Database and Information Systems. | Subarea 5 |
| SS | Software Systems. | Subarea6 |
| TCS | Theoretical Computer Science. | Subarea 7 |
Next, we select six widely used Scientometrics Indicators (SIs), namely CiteScore, h5-index, h-index, ImpactScore, Source Normalized Impact per Paper (SNIP), and SCImago Journal Rank (SJR), as in Table 2. We assess the widely varying ranges of these selected indicators for these subfields and the correlation among them. We use the K-means[20,21] cluster algorithm and decompose the scientometrics space of the chosen CS subareas into clusters. The purpose is to split the indicator ranges into multiple regions using clustering. We empirically analyze six indicators of the seven CS subareas to address the following Research Questions (RQs):
RQ1: Does the correlation of scientometrics indicators show any subarea-specific patterns? Is such correlation specific to the chosen indicator and the subarea?
RQ2: Does the clustering with two or more scientometrics indicators show subarea-specific patterns? Can the clustered sub-spaces be used as partitioning of subarea-specific indicator values and their ranges?
This research study is focused on subarea-specific scientometrics indicators. The research contributions of this study, addressing the above questions, are the following:
The subarea-specific scientometrics indicators are highly correlated; however, such correlation varies from subarea to subarea, and The combined use of indicators across the CS subfields shows distinctive patterns. The subfield-specific indicator ranges are split into multiple subspaces using clustering. The clustered subfield-specific indicators show distinctive patterns across subfields.
Such findings imply that a subset of indicators may not be equally suitable for all subareas as the indicators are subarea dependent. The K-means clustering results are stable across varying values of K.
The rest of the paper is organized as follows. We discuss indicators and related work specific to CS research in Section 2. Section 3 includes the focus of the study and the data sources used in this study. In Section 4, we elaborate on the proposed methodology. We assess the relationship between indicators and inter- and intra-cluster analysis in Section 5. Finally, we conclude the findings of this study and future work in Section 6.
LITERATURE REVIEW
In the past, several quantitative and qualitative methods have been used to analyze the publication data. Mainly, researchers have proposed various indicators and utilized such indicators to quantify the impact of publication venues. We have grouped related work into two subsections: (i) indicators for publication venues and (ii) scientometrics studies specific to CS research.
| Indicators | Database |
|---|---|
| CiteScore | Scopus |
| h-index | Scopus |
| h5-index | Google Scholar |
| ImpactScore | Scopus |
| Source Normalized Impact per Paper (SNIP) | Scopus |
| SCImago Journal Rank (SJR) | Scopus |
Indicators for Publication Venues
The basis indicators of research publications are the number of publications and citation count. Using such fundamental indicators, researchers, institutions, and databases have proposed several other metrics to evaluate the publication venues. The Impact Factor is a widely used metric to assess the journals.[6,7] It is easy to calculate and use. The Impact Factor remains the most popular indices to quantify journals based on a 5-year or 2-year citation window. Various other indicators have been proposed considering such metrics, e.g., cited half-life, Eigen Factor, h-index, etc.[8–10] Different publication houses or database holders developed other emerging metrics, such as CiteScore, SJR, SNIP, h5-index, etc.[11,12] The CiteScore is used to quantify Scopus-based journals. However, the Eigen Factor is considered more robust than the Impact Factor for measuring a journal’s importance. The h-index is used for assessing individuals and journal publications both.
In addition, Google Scholar proposed two metrics for publication venues: the h5-index and the h5-median. The h5-index is the largest h calculated based on the last 5-year window. For example, an h5-index of fifty means the selected venue has published fifty articles in the previous five years with fifty or more citations each. However, h5-median calculates the middle value of citations for the h number of citations. Based on Scopus data, ImpactScore considers a 2-year citation window. These indicators are widely used and considered an essential component of the scientific domain.
These numerous indicators are widely used in various assessment processes. Though these metrics have several advantages still, these indicators have several shortcomings.[9,22] For example, the Impact Factor of a journal is driven by a small number of highly cited studies;[23] it can be influenced and biased by the nature of the subfield.[18] The Eigen factor is based on the journal’s size and cannot differentiate document types in its calculation. Moreover, the calculation of SNIP includes a more complex methodology and does not differentiate between the prestige of citations. The number of publications limits the h-index and h5-index. Despite several usages, these indicators are limited by several factors. For example, most indices may show bias due to self-citation and inability to cross-disciplinary comparisons.[22–24] It is incapable of differentiating performance from equal values. Such indicators consider different parameters, citation windows, and databases. Furthermore, the indicators using citation count as a journal’s impact may be misleading in several scenarios.[25] Moreover, studies also concluded that a single metric might not be suitable for evaluation.[17]
For example, various other studies have also been done regarding influencing factors of citation impact and others. The prominence of journals also depends on multiple factors, i.e., funding agency, promotion, collaboration behavior, and others. Some journals reflect high quality based on their citation impact. The study concluded that the funding influences the citation impact in CS.[26] The citations count per paper of a funded paper is significantly higher than non-funded papers in CS research.[27] In addition, there are several other issues, for example, (i) papers in Open-Access Journals (OAJ) attract higher citations, (ii) supremacy of CS conference over journal publications, (iii) prominence of journals with factors such as funding, collaborative research, etc. Several studies highlighted or addressed such issues.[26–28] However, these are not the focus of this study, and we are not addressing these issues in this study.
Scientometrics Studies of CS Research
Several studies have been done to quantify the impact of CS research publications. In the main, Serenko[3] ranked 182 journals of Artificial Intelligence (AI) based on citation-based indices, i.e., h-index, g-index, and hc-index. They concluded that ranking based on such metrics correlated perfectly with one another and strongly correlated with the journal Impact Factor. Further, the study considered the survey-based approach for developing the ranking of AI journals. Such a ranking was also compared with citation-based ranking and found to be moderately correlated. Researchers also concluded that these two ranking methods could not be considered substitutes; instead, they should be used as complementary.[5]
Tsai[4] assessed the correlation between the Impact Factor and h-index for journals of five CS subareas. They found that the correction is low between such indicators. Researchers have re-ranked the journal based on the CombSum method. Despite the single use of metrics, studies also utilized the combined indicators for assessing the journal publications. In contrast, our study in this paper has shown high correlation between some indicators and lower for others. We argue that the correlation is specific to some chosen CS subareas as well as some selected indicators.
In addition, Haddawy et al.[29] studied the relation between three citation metrics, e.g., SNIP, RIP, JIF, and human expert judgment. They suggested that the SNIP indicator may be better than other indicators. Moreover, Halim and Khan[19] proposed a data science-based framework and utilized nineteen bibliometrics indicators for assessing journal publications. Their framework considered three feature selection techniques: two clustering techniques and two classifiers. Using these indicators and methods, they have categorized computer science journals into various groups.
Motivated by such research, this study explores scientometrics indicators of seven subareas of CS research. We assess the correlation among indicators and analyze the natural grouping of SIs of CS subareas journals using K-means clustering.
STUDY FOCUS AND DATA SOURCES
Study Focus
Most of the scientometrics indicators are based on citation count. However, the citation patterns vary from one subarea to another subarea. For instance, several subareas of Computer Science are cited more often than others. Thus, scientometrics values vary across the CS subfields. This section shows the scientometrics of journals chosen from seven diverse subareas of CS. It can be observed from Figure 1 that the higher range of indicators value corresponds to both CNWC and CVPR subareas (for abbreviations, refer to Table 1). However, when we analyze the indicators’ value more subtly, we find that CNWC and CVPR subareas can be easily differentiated based on the h5- and h-index. The journals of the CNWC subfield show a high range of indicators’ values for almost all of the metrics except these two (h5-index and h-index). While in the case of the CVPR subarea, the inference is exactly the opposite.
Although, for other subareas, chosen metrics have a lower range. The journals of subareas, e.g., SS, CG, TCS, and DBIS, have a highly diverse range of indicators. Some indicators’ values corresponding to these subareas are significantly very low compared to the other subareas. Especially, Figures 1a and 1f show that the CiteScore and h5-index of TCS journals are substantially lower than journals of other subfields. Despite the low scientometrics values of the TCS subarea, a few of its journals belong to top-tier venues in the CS discipline. This is due to the fact that the TCS subarea is a highly specialized research area despite its lower scientometrics values.
The above findings indicate that the publishing behavior of CS research differs widely in the context of subareas; their scientometrics vary widely, and thus we cannot generalize the impact of journals across all the subareas. Therefore, we argue that the scientometrics analysis across the CS discipline may not reflect an accurate picture. Instead, we should study the scientometrics profile of journals inside their respective subareas. In addition, assessing journals from diverse backgrounds based on multiple indicators or their valid combinations is more intuitive to achieve more appropriate results. In this study, we use six scientometrics indicators and assess the impact of journals of seven subareas based on the combined use of indicators.
Scientometrics Data Sources
Google Scholar maintains the rank of the Top 20 venues each, i.e., conferences, journals, workshops, etc., of several disciplines and their subcategories. We select seven CS subareas from this data source, as in Table . We consider only journal publications of CS within the Top 20 venues ranked by Google Scholar. Journals from their corresponding subareas used in this study are listed in Tables 3 to 9. One table is used for each of the seven subareas, namely, Artificial Intelligence/Machine Learning (AI/ML), Computer Networks and Wireless Communication (CNWC), Computer Vision and Pattern Recognition (CVPR), Computer Graphics (CG), Database and Information Systems (DBIS), Software Systems (SS), and Theoretical Computer Science (TCS). For selected journals, we gathered six indicators for each journal. Such journal indicators are h5-index, h-index, ImpactScore, SCImago Journal Rank (SJR), Source Normalized Impact per Paper (SNIP), and CiteScore (Tables 3 to 9). These indicators have been gathered from different publicly available sources. For example, the h5-index is collected from the Google Scholar website. 1 Moreover, the h-index is gathered from SCImago,2 and ImpactScore from the resurchify website.3 The SJR, SNIP, and CiteScore are taken from the Scopus database.4 In this study, we have taken the latest values of these indicators of the seven CS subareas as available while writing this paper in the year 2022

Figure 1:
Range of six scientometrics indicators from seven subfield-specific CS journals
THE PROPOSED METHODOLOGY
Based on scientometrics indicators of journals, this study focuses on the relationship between indicators and the natural grouping of journals using clustering. Since journal indicators vary across subareas of the CS domain, analyzing the impact of journals from different CS subareas is essential. Additionally, the journal’s impact assessment should be done based on the combined use of indicators. We, in this study, explore the correlation between the indicators with respect to each chosen subarea. We choose Pearson’s Correlation Coefficient for carrying out such an analysis. We explore the relationship between indicators and assess highly correlated indicators for each chosen subarea based on such a method. Moreover, this study also utilizes six indicators for each subfield-specific journal. However, the combined analysis of journal indicators requires their meaningful grouping.
Second, we explore the natural grouping of subarea journals through empirical analysis. We consider K-means clustering for the natural grouping of journals based on the diverse scientometrics of CS journals. We choose K-means[20,21] clustering, a well-known unsupervised Machine Learning technique that can effectively organize the data into natural groups. The clusters will indicate splitting the indicator ranges into regions based on the natural grouping of the clustering techniques. This could be used in multiple applications; one trivial use is quality quartiles of research publications. Thus, this study aims to assess whether the natural grouping of subfield-specific journals shows any distinct subfield-specific pattern. We use the most popular clustering method, i.e., K-means clustering. We used the initial value of K as four and kept increasing the K value up to 7.
In this study, clusters consider the combined use of two and six indicators of journals for its formation. Further, we analyze the inter- and intra-cluster with the proportion of subarea-wise journals. We compute the proportion of journals for each cluster with respect to K in the range of K= 4 to 7; however, we include the results for K = 6 and 7. We conduct our study in the following steps, as depicted in the flowgraph, Figure 2:
Step I: Select journals and collect their scientometrics Indicators.
Step II: Compute the correlation coefficient for pair-wise indicators. Plot correlation heatmap of chosen subareas.
Step III: Apply K-means algorithm to collected data. Start with K=4 with an increment of one in K values to 7 (results are reported for K= 6 and 7).
Step IV: Form clusters based on the combined use of two and six journal indicators.
Step V: Carry inter- and intra-cluster analysis considering the proportion of subarea-wise journals in each cluster.
Step VI: Find out subarea-specific clusters. Assess the distinctive patterns across subfields and analyze them.
In summary, this study assesses the different clusters of journals of the chosen subareas formed by the K-means algorithm.
RESULTS AND DISCUSSION
We, in this section, empirically analyze the correlation between subarea indicators and their natural grouping with clustering. In the first subsection, we present the correlation between pair-wise indicators of the chosen subareas. Then, in the following subsection, we apply the clustering and interpret the clusters so formed for their inter- and intra-cluster proportions of various journals. Finally, we discuss the finding of this work.
Correlation of Scientometrics Indicators of CS Subareas
Based on the collected data, we compute the Pearson correlation coefficient for pair-wise indicators. Figure 3 depicts the correlation heatmap of seven subareas of CS. It can be seen that highly correlated indicators vary from subarea to subarea. For example, CiteScore and SJR are highly correlated in AI/ML (0.99) and DBIS (0.97) subareas. However, we can notice the highest correlation is 1 for the CNWC subfield (Figure 3c) for three pair-wise indicators.
Similarly, a high correlation between ImpactScore and CiteScore (0.96) can be seen for the CG subarea. Other indicators are also correlated for the CG subarea with a marginal difference (Figure 3b). The correlation coefficient between the h5-index and CiteScore of the SS subfield is 0.96. The remaining CVPR subarea has a high correlation (0.97) for CiteScore and SNIP metrics. Figure 3d shows that the indicators SNIP vs. ImpactScore and SJR vs. ImpactScore have a higher correlation for the TCS subfield, and so on. These findings indicate that for most subareas, highly correlated variables vary from subarea to subarea. Moreover, such results also imply that significant diversity exists in subareas of CS, and hence no single measure can be said equally suitable for all the subareas.
Inter-and Intra-Cluster Analysis
Based on the collated data of seven subareas (Tables 3 to 9) for exploring the different natural grouping of journals, we apply the K-means algorithm to exhibit the clusters set and analyze journals’ natural grouping in different subareas. We conduct inter- and intra-cluster assessments based on the resultant clusters and the proportion of subfield-specific journals. We mainly compute the proportion of subarea-wise journals in each cluster. Initially, we form clusters by utilizing the combined use of two indicators. Further, we analyze the clusters with respect to the combined use of all six indicators.
| Sl.No. | Journals (AI/ML) | h5 | h-index | ImpactScore | SNIP | SJR | CiteScore |
|---|---|---|---|---|---|---|---|
| 1 | Expert Syst. Appl. | 132 | 225 | 9.60 | 2.985 | 2.078 | 12.2 |
| 2 | IEEE Trans. Neural Netw. Learn. Syst. | 132 | 221 | 10.47 | 3.306 | 4.222 | 20.8 |
| 3 | Neurocomputing | 123 | 157 | 6.19 | 1.66 | 1.85 | 10.3 |
| 4 | Appl. Soft Comput. (ASOC) | 112 | 156 | 9.03 | 2.396 | 1.959 | 12.4 |
| 5 | Knowledge-Based Syst. | 107 | 135 | 8.66 | 2.611 | 2.192 | 12.0 |
| 6 | IEEE Trans. Fuzzy Syst. | 101 | 191 | 11.84 | 3.143 | 4.08 | 21.9 |
| 7 | Neural Comput. Appl. | 99 | 94 | 5.6 | 1.653 | 1.072 | 8.7 |
| Sl.No | Journals (CG) | h5 | h-index | ImpactScore | SJR | SNIP | CiteScore |
|---|---|---|---|---|---|---|---|
| 1 | ACM Trans. Graphics (TOG) | 103 | 221 | 7.71 | 2.676 | 7.148 | 14.2 |
| 2 | IEEE Trans. Visual. Comput. Graphics | 85 | 148 | 5.56 | 2.431 | 1.753 | 11.4 |
| 3 | Comput. Graphics Forum | 58 | 121 | 2.66 | 1.29 | 1.668 | 5.4 |
| 4 | The Visual Comput. | 36 | 69 | 3.02 | 1.211 | 0.658 | 4.0 |
| 5 | Comput. and Graphics | 30 | 74 | 1.88 | 1.07 | 0.925 | 5.3 |
| 6 | IEEE Comput. Graphics Appl. | 30 | 95 | 2.11 | 0.98 | 0.686 | 3.9 |
| 7 | Comput. Aided Geometric Design | 22 | 72 | 1.35 | 1.118 | 0.633 | 3.0 |
| Sl.No. | Journals (CNWC) | h5 | h-index | ImpactScore | SNIP | SJR | CiteScore |
|---|---|---|---|---|---|---|---|
| 1 | IEEE Commun. Surv. and Tutorials | 159 | 216 | 39.97 | 11.315 | 13.519 | 69.4 |
| 2 | IEEE Trans. Veh. Technol. | 128 | 188 | 7.11 | 1.894 | 2.515 | 11.9 |
| 3 | IEEE Trans. Wireless Commun. | 118 | 224 | 9.6 | 2.321 | 4.436 | 15.7 |
| 4 | IEEE J. Sel. Areas Commun. | 107 | 242 | 14.24 | 3.559 | 6.32 | 21.2 |
| 5 | IEEE Trans. Commun. | 103 | 216 | 7.04 | 1.873 | 3.106 | 11.3 |
| 6 | IEEE Wireless Commun. | 93 | 169 | 13.43 | 3.376 | 6.06 | 22 |
| 7 | J. of Network and Comput. Appl. | 90 | 115 | 9.29 | 2.512 | 2.193 | 15.7 |
| Sl.No | Journals (CVPR) | h5 | h-index | ImpactScore | SNIP | SJR | CiteScore |
|---|---|---|---|---|---|---|---|
| 1 | IEEE Trans. Patt. Anal. Mach. Intell. | 165 | 377 | 15.84 | 7.338 | 8.269 | 36.6 |
| 2 | IEEE Trans. Image Process. | 128 | 296 | 9.74 | 3.131 | 4.03 | 16.4 |
| 3 | Pattern Recognit. | 110 | 280 | 21.94 | 3.089 | 3.113 | 15.5 |
| 4 | Medical Image Analysis | 90 | 143 | 15.24 | 4.042 | 4.172 | 15.6 |
| 5 | Int. J. Comput. Vision | 75 | 201 | 11.81 | 4.168 | 6.838 | 16.8 |
| 6 | Pattern Recognit. Lett. | 72 | 163 | 5.67 | 1.786 | 1.479 | 8.6 |
| 7 | Comput. Vision Image Understanding | 53 | 139 | 5.53 | 1.928 | 1.916 | 9.9 |
| Sl.No. | Journals (DBIS) | h5 | h-index | ImpactScore | SNIP | SJR | CiteScore |
|---|---|---|---|---|---|---|---|
| 1 | IEEE Trans. Knowledge Data Eng. | 88 | 183 | 6.09 | 3.619 | 2.431 | 13.1 |
| 2 | Information Processing Management | 70 | 104 | 8.2 | 3.01 | 1.854 | 11 |
| 3 | Journal of Big Data | 55 | 45 | 14.57 | 4.661 | 2.592 | 14.4 |
| 4 | Knowledge and Information Syst. | 51 | 78 | 3.06 | 1.413 | 0.988 | 5.9 |
| 5 | IEEE Trans. on Big Data | 45 | 10 | 2.6 | 1.791 | 0.656 | 6.9 |
| 6 | Information Systems | 44 | 88 | 3.65 | 1.903 | 1 | 7.1 |
| 7 | Semantic Web | 43 | 45 | 3.59 | 2.929 | 1.242 | 7.8 |
| Sl.No. | Journals (SS) | h5 | h-index | ImpactScore | SNIP | SJR | CiteScore |
|---|---|---|---|---|---|---|---|
| 1 | IEEE Trans. Software Eng. | 66 | 173 | 5.25 | 3.355 | 2.027 | 11.4 |
| 2 | J. of Syst. Software | 61 | 113 | 4.48 | 2.157 | 1.418 | 8.9 |
| 3 | Information and Software Tech. | 59 | 107 | 4.77 | 2.271 | 1.446 | 9.1 |
| 4 | Empirical Software Eng. | 56 | 79 | 4.6 | 2.458 | 1.89 | 8.2 |
| 5 | IEEE Software | 47 | 116 | 2.11 | 1.897 | 1.115 | 6.1 |
| 6 | Software and Systems Modeling | 40 | 52 | 2.87 | 1.744 | 0.833 | 6.0 |
| 7 | Software- Practice and Experience | 34 | 71 | 3.34 | 1.119 | 0.774 | 4.8 |
| Sl.No | Journals (TCS) | h5 | h-index | ImpactScore | SNIP | SJR | CiteScore |
|---|---|---|---|---|---|---|---|
| 1 | J. ACM (JACM) | 39 | 131 | 2.87 | 2.853 | 2.808 | 6.7 |
| 2 | SIAM J. Comput. | 38 | 116 | 2.35 | 1.921 | 2.349 | 4.4 |
| 3 | Theor. Comput. Sci. | 35 | 119 | 1.29 | 1.056 | 0.621 | 2.1 |
| 4 | ACM Trans. on Algorithms | 33 | 52 | 1.84 | 1.725 | 1.783 | 3.7 |
| 5 | J. of Automated Reasoning | 28 | 56 | 1.66 | 1.411 | 0.93 | 4.2 |
| 6 | Algorithmica | 28 | 75 | 1.31 | 1.236 | 0.958 | 2.7 |
| 7 | J. of Comput. and Syst. Sci. | 27 | 96 | 1.29 | 1.305 | 0.861 | 3.1 |
Combination of Two Indicators
Clustering using a single scientometrics indicator is trivial. It is shown in Figure 1 that most single indicator varies widely across the chosen subareas. This is consistent with the inference of the study conducted by other researchers that single indicators might not be suitable for the evaluation process.[17,18] Therefore, we cluster the data by combining two indicators each. We studied the clustering for all combinations of two indicators at a time; however, we have included results of h5-index and SNIP only in the following paragraphs. The clustering results of other combinations were almost similar.
We have experimented with the values of K in the range of 4 to 7. In this section, we include the results for K = 7 in Figure 4, in which we plot the clusters using h5 and SNIP indicators for seven subfields. Findings indicate that combined SNIP vs. h5-index use groups the subfield-specific journals effectively. Figure 4 shows the proportion of subfield-wise journals for each cluster. For example, Cluster_0 has groups of five subareas journals. Cluster_1 has three subarea-specific journals. Cluster_2 and Cluster_4 are singletons containing only one subarea. Cluster_2 contains journals of CNWC, and Cluster_4 groups the CVPR subarea. Cluster_3 and Cluster_5 have clustered journals of four
| Two SIs | Six Scientometrics Indicators (SIs) | ||
|---|---|---|---|
| Subfields | K = 6 | K= 6 | K = 7 |
| AI/ ML | 2 (Mixed) | 3 (Mixed) | 3 (Mixed) |
| CG | 3 (Mixed) | 4 (Mixed) | 3 (Mixed) |
| CNWC | 1 (Singleton), 3 (Mixed) | 1 (Singleton), 3 (Mixed) | 1 (Singleton), 2 (Mixed) |
| CVPR | 1 (Singleton), 4 (Mixed) | 1 (Singleton), 3 (Mixed) | 1 (Singleton), 2 (Mixed) |
| DBIS | 2 (Mixed) | 2 (Mixed) | 1 (Singleton), 3 (Mixed) |
| SS | 2 (Mixed) | 2 (Mixed) | 2 (Mixed) |
| TCS | 2 (Mixed) | 2 (Mixed) | 2 (Mixed) |
| (Figure 4) | (Figure 5) | (Figure 6) |
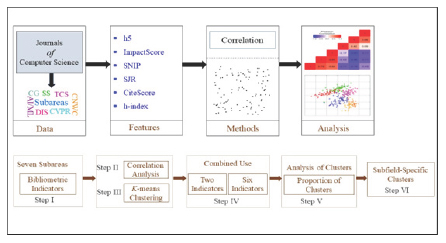
Figure 2:
A schematic showing the workflow of the proposed methodology. subfields. Cluster_6 has grouped journals of three subfields. Thus, the AI/ML subfield is in clusters {3,6}; the CG subfield is in the cluster {0,1, and 3}; the CNWC is in clusters {2,3,5, and 6}; the CVPR subfield is in clusters {0,3,4,5, and 6}; the DBIS subfield is in the clusters {0,5}; the SS subfield is in the cluster {0,1, and 5}; the TCS subfield is in the cluster {0,1}
Combined Use of All Six Indicators
We have done clustering based on some combinations of three and more indicators. However, the findings are not much distinct. Therefore, in this subsection, we present the clustering results done on the data using all six indicators. We experimented with the K-means clustering for different values of K; however, we got meaningful grouping results for K values of 6 and 7. Therefore, we include the results for K=6 and K=7 in Figures 5 and 6. The proportion of each subarea-specific journal within each cluster is shown in these figures. Initially, for K=6, we find clusters where two clusters contain singleton subfields and others have mixed clusters. Figure 5 shows that Cluster_0, Cluster_2, Cluster_3, and Cluster_5 have grouped journals from multiple subfields. However, Cluster_1 and Cluster_4 are singleton clusters. Thus, from Figure 5, we can observe that the AI/ML subfield is in clusters {0, 3, 5}; the CG subfield is in clusters {0, 2, 3 and 5}; the CNWC is in clusters {0, 1, 3, and 5}; the CVPR subfield is in clusters {0, 2, 3, and 4}; the DBIS subfield is in the clusters {0, 5}; the SS subfield is in the clusters {0, 2}; the TCS subfield is in the clusters {0, 2}.
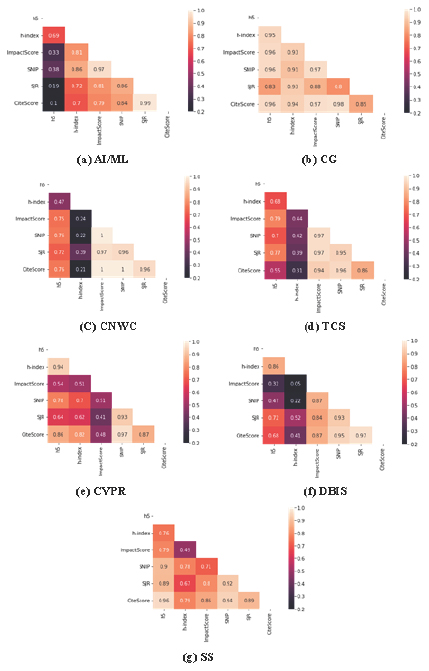
Figure 3:
Correlation of indicators using heatmap
In addition, to show the difference in results of varying K values, we also plot pie charts for K=7. Figure 6 shows that a few clusters
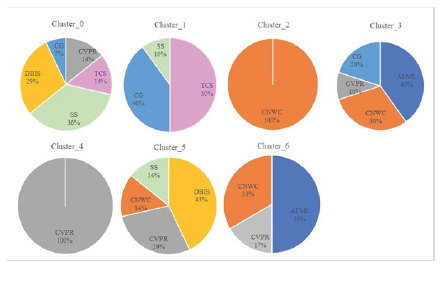
Figure 4:
Proportion of subfield-specific journals using h5 vs. SNIP

Figure 5:
Proportion of subarea-specific journals with the combined use of six indicators for K=6
contain only one subarea. For example, Cluster_2, Cluster_3, and Cluster_4 contain CNWC, CVPR, and DBIS subfields, respectively. However, the clusters with CNWC and CVPR are always stable for the covered subarea despite varying K values. Cluster_0, Cluster_1, Cluster_5, and Cluster_6 have clustered journals from different subfields.
These findings conclude that for K=6, two singletons and the rest are mixed clusters. As we increase the K value (K=7), the number of singleton clusters increases to three. Such findings convey that indicators vary across the subareas of CS. Moreover, these results suggest that the indicators are subarea dependent with varying ranges and patterns.
We summarize the K-means clustering results in Table 10 in Figures 4, 5, and 6. From the table, a systematic pattern could be observed that the clustering results are almost stable across the scientometrics indicators and the number of clusters.
Interpretation of the proposed clustering
One basic use of scientometrics indicators is assessing publication venues’ impact. This subsection analyzes the impact of clustering
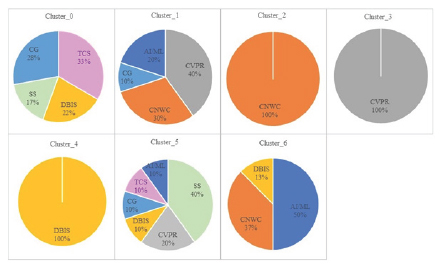
Figure 6:
Proportion of subarea-specific journals with the combined use of six indicators for K=7
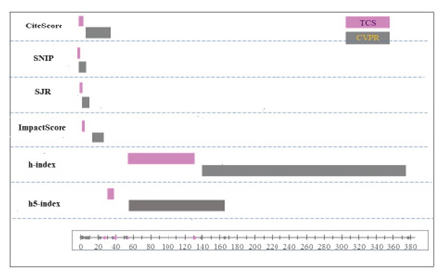
Figure 7:
Range of indicators of TCS and CVPR subfields-specific journals. the subfield-specific indicators. We have already shown that the scientometrics indicators vary widely; the same is the case with the ranges of the indicators for the CS subfields. For example, kindly refer to the ranges of all indicators for two subfields, TCS and CVPR, shown in Figure 7. The values of all indicators for the TCS subfield are located on the left side of the figure and have narrow ranges of lower values, while the same indicators for the CVPR subfield are much wider with large values; especially the h and h5- indices have much wider ranges for the CVPR field
The above pattern of indicators is reflected in the clusters, as obtained in Figures 4, 5, and 6. The clusters in Figure 4 considered only two indicators, namely, h5-index and SNIP. As shown in Figure 7, the SNIP values of the TCS and CVPR subfields have some overlap, while SNIP values are distinct. The same overlap is reflected in (Figure 4) Cluster_0, and the distinctiveness of SNIP is reflected in Cluster_1 (only TCS) and Cluster_3, Cluster_4, Cluster_5, and Cluster_6; none of these has any sharing with TCS (Figure 4). The Cluster_4 (Figure 4) is a singleton, indicating that these indicators are not shared with any other subfield.
The clustering results using all six indicators are shown in Figures 5 and 6 for K=6 and 7, respectively. For these two subfields, TCS and CVPR, the SNIP and SJR indicators are partly (Figure 7), while all other indicators for the CVPR subfield have much higher values and wider non-overlapping with the TCS subfield. These overlapping patterns of these indicators are reflected in Cluster_0 and Cluster_2 (Figure 5), and Cluster_5 in Figure 6. The distinctiveness patterns of TCS over CVPR is reflected in Cluster_0 (no CVPR) of Figure 6. The distinct characteristics of CVPR over TCS are in Cluster_3 and Cluster_4 (Figure 5), and Cluster_1 and Cluster_3 (Figure 6); the Cluster_4 (Figure 5) and Cluster_3 (Figure 6) are singleton. Similarly, the overlapped and distinctiveness of scientometrics indicators across all the other five subfields could be analyzed based on these clustering results. Thus, the above clustering results indicate that the publications of the same subfield are clustered into multiple clusters. The formed clusters split each CS subarea’s wide spectrum of scientometrics indicators into multiple regions/groups. In this way, clustering using various subfield indicators shows the natural grouping of publications. We observe, A single subfield is clustered into multiple clusters, A few clusters comprise a single subfield, while most have multiple subfields.
The above is shown to happen with all subfields (Table 10). The CVPR subfield has a large range of indicators, so such a subfield has more clusters; this is grouped into 3 to 5 clusters. Out of which, one cluster is monolithic and distinct, and others have mixed behavior. The TCS subfield clustered into two clusters only (Figures 4, 5, and 6; Table 10) due to smaller values with narrower ranges. Similarly, all the other subfields and their clustering impact based on their indicators could be analyzed.
We can infer interesting observations from the above. For example, the Theoretical Computer Science Journal is highly impactful among researchers despite its low range of indicators. Thus, by such analysis, we can identify the TCS subfield-specific publications and have their own clusters partitioning their subspaces into multiple clusters. This phenomenon reiterates that The scientometrics indicators are subfield specific; their values and ranges have distinctive patterns over other subfields, and The scientometrics space of a particular CS subfield could be further partitioned into sub-spaces.
In this work, we have obtained partitioned subspaces overlapped with other subfields (mixed clusters) or non-overlapped (singleton clusters). We have analyzed the overlapping behavior due to the overlapped values and ranges of their respective indicators. In the future, we wish to investigate further partitioning the mixed clusters using hierarchical clustering techniques.[30–32]
However, the mixed clustering results obtained in this work are no hindrance to possible usages and interpretation of the subfield-specific indicators. Such partitioning or grouping of indicators into smaller subspaces could probably be used for quality quartiles of subfield-specific publications. For example, TCS subfield-specific quality quartiles are defined with their lower values of indicators. TCS publications fall in a lower quality quartile on the total spectrum of scientometrics indicators of CS. However, such clustering and labeling of their TCS subfield-specific clusters, based only on their indicator ranges/ values, will make an independent quality quartiles of TCS publications.
Similarly, the other higher indicator ranges/values of CVPR, CNWC, etc. will make their own subfield-specific clusters and their labeling to their own quality quartiles (e.g., Q1, Q2, Q3, etc.) instead of having integrated Quartiles defined for the whole CS publications. Such multiple clusters of a single subfield categorize the subfield-specific publications into multiple quartiles. Thus, each subspace of a specific subfield could be used as a quality quartile for its own.
DISCUSSION
Journals are the sole medium of publication in most scientific disciplines. Several indicators exist for assessing journal publications; these metrics are limited due to several factors. Moreover, publication practices and their readerships differ significantly across the discipline and the subareas of a discipline. Due to differences in citation practices and publication patterns, scientometrics indicators widely vary from discipline/subareas. Such differences can also be seen in different subareas of the CS discipline.
For instance, CNWC and CVPR subareas represent a significantly higher range of indicators than other chosen subareas (Figure 1 and 7). On the contrary, the TCS subfield shows a lower range of metrics values. However, the fact is that some of the journals in the TCS category are termed high-quality journals worldwide. Due to such reasons, the combined use of indicators is an appropriate way to assess the impact of journals. Therefore, this paper uses combined indicators to assess the various scientometrics indices of different subareas. We have included journals from seven subareas listed in the Top 20 venues of Google Scholar and considered six indicators for each journal.
Concerning the Research Question (RQ1)
“Does the correlation of scientometrics indicators show any subarea-specific patterns? Is such correlation specific to the chosen indicator and the subarea?” This study presents a correlation coefficient for pairwise indicators based on the scientometrics indicators of seven subfield-specific journals. Figure depicts the correlation heatmap, indicating scientometrics strongly correlates among subareas. However, highly correlated indicators vary for most of the subareas. Such correlation finding indicates patterns vary across chosen subareas; hence, no single measure can be considered equally suitable for all the subareas. Other researchers have done correlation analysis in the past, which is limited by subareas and selected indicators. For example, Serenko[3] presented rank correlation for AI journals using four indicators: h-index, g-index, hc-index, and Impact Factor. Tsai[4] took a few subfields, namely, AI, IS, SS, etc., with Impact Factor and h-index. The correlation analysis presented in this paper is generalized; it uses a wider range of most commonly used indicators over major CS subareas. The subfield-specific journals are collected for the Top 20 venues of Google Scholar, the widely used and most populated data source.
Concerning the Second Research Question (RQ2)
“Does the clustering with two or more scientometrics indicators show any sub-area specific patterns? Can the clustered sub-spaces be used as partitioning of subarea specific indicator values and their ranges?” Addressing this research issue, we apply K-means clustering on different journal indices to find natural grouping among them. The purpose of partitioning the subfield-specific indicators was to move one step ahead, showing that the combined use of indicators effectively categorizes subfield-specific publications. We observe the clustering results to be stable across combinations of indicators and the number of partitions as emerged from the clustering (Table 10). It is evident from the clustering results that the journals belonging to different subareas show distinctive patterns across subfields; some partitions are singleton, and most are mixed. The indicators are influenced significantly by the nature of the study subareas. The journals belonging to different subareas show distinctive patterns across subfields. The indicators are influenced significantly by the nature of the study subareas, followed by a detailed description of Table 10 and Figure 7 in the subsections of the result section.
This study uses K-means clustering to decompose the CS subareas’ scientometrics space. However, a more appropriate methodology, e.g., hierarchical clustering, for partitioning the indicator subspaces could be explored in future. A more effective grouping of cases where multiple subfields share the same indicator spaces is also the topic of future research. This will incorporate the use of various other forms of advanced clustering techniques with the inclusion of a more detailed ML paradigm. This knowledge may be used as a signature for partitioning the subarea-specific indicators and their possible future uses.
CONCLUSION
This study analyzed multiple commonly used scientometrics indicators of research publications in seven subareas of the CS discipline. The study reiterated that indicator values vary significantly from subarea to subarea. In addition, multiple indicators or combinations should be used to quantify the publications instead of a single indicator. For this, we collected six scientometrics indicators for each publication, conducted the correlation analysis, and applied clustering to analyze the subspace patterns of subarea-specific grouping.
The correlation analysis infers that the high correlation between different combinations of indicators is random in terms of the diversity in the subareas. Different subareas show a high correlation between different combinations of indicators. Moreover, based on our inter- and intra-cluster analysis, we infer that a few clusters are monolithic while most others have mixed subfields. The combined use of six indicators shows distinctive patterns across the subfields of CS. Thus, a single measure may not be suitable for assessing the journals of all the subareas. The study infers that the scientometrics indicators are subarea-dependent, and the combined use of indicators is more appropriate for determining the impact of journals.
This study is restricted to the seven CS subareas; this could be extended to more subareas to generalize findings. This work could also be extended by employing advanced clustering techniques and algorithms within a detailed machine-learning framework. A comprehensive correlation analysis leading to the dimensionality reduction, followed by clustering into the meaningful subarea’s natural grouping, is another area of future work. The obtained partitioned ranges of subarea-specific scientometrics indicators could be labeled effectively and more meaningful for various applications, such as identifying quality quartiles for each subarea-specific publication. The study may be further extended to other disciplines of Arts, Science, Social Sciences, Engineering, etc., and their subareas.
Cite this article
Kumari P, Kumar R. Clustering Scientometrics of Computer Science Journals for Subarea Decomposition. J Scientometric Res. 2023;12(2):383-94.
ACKNOWLEDGEMENT
The authors thank the reviewers for their valuable comments. They also thank the Journal Manager and the editorial staff for managing this manuscript.
References
- Muhuri PK, Shukla AK, Janmaijaya M, Basu A. Applied soft computing:A bibliometric analysis of the publications and citations during (2004–2016). Applied Soft Computing. 2018;69:381-92. [Google Scholar]
- Espinoza-Audelo LF, León-Castro E, Mellado-Cid C, Merigo JM, Blanco-Mesa F. Uncertain Induced Prioritized Aggregation Operators in the Analysis of the Imports and Exports. Journal of Multiple-Valued Logic and Soft Computing. 2021;36(6) [Google Scholar]
- Serenko A. The development of an AI journal ranking based on the revealed preference approach. Journal of Informetrics. 2010;4(4):447-59. [Google Scholar]
- Tsai CF. Citation impact analysis of top ranked computer science journals and their rankings. Journal of Informetrics. 2014;8(2):318-28. [Google Scholar]
- Serenko A, Dohan M. Comparing the expert survey and citation impact journal ranking methods:Example from the field of Artificial Intelligence. Journal of Informetrics. 2011;5(4):629-48. [Google Scholar]
- Garfield E. Citation analysis as a tool in journal evaluation:Journals can be ranked by frequency and impact of citations for science policy studies. Science. 1972;178(4060):471-9. [Google Scholar]
- Garfield E, Sher IH. New factors in the evaluation of scientific literature through citation indexing. American documentation. 1963;14(3):195-201. [Google Scholar]
- Braun T, Glänzel W, Schubert A. A Hirsch-type index for journals. Scientometrics. 2006;69(1):169-73. [Google Scholar]
- Kim K, Chung Y. Overview of journal metrics. Science Editing. 2018;5(1):16-20. [Google Scholar]
- Alonso S, Cabrerizo FJ, Herrera-Viedma E, Herrera F. h-Index:A review focused in its variants, computation and standardization for different scientific fields. Journal of informetrics. 2009;3(4):273-89. [Google Scholar]
- Fang H. Analysis of the new Scopus CiteScore. Scientometrics. 2021;126(6):5321-31. [Google Scholar]
- González-Pereira B, Guerrero-Bote VP, Moya-Anegón F. A new approach to the metric of journals’ scientific prestige:The SJR indicator. Journal of informetrics. 2010;4(3):379-91. [Google Scholar]
- Yu D, Shi S. Researching the development of Atanassov intuitionistic fuzzy set:Using a citation network analysis. Applied Soft Computing. 2015;32:189-98. [Google Scholar]
- Cobo MJ, Martínez MÁ, Gutiérrez-Salcedo M, Fujita H, Herrera-Viedma E. 25 years at knowledge-based systems:a bibliometric analysis. Knowledge-based systems. 2015;80:3-13. [Google Scholar]
- Yu D, Xu Z, Kao Y, Lin CT. The structure and citation landscape of IEEE Transactions on Fuzzy Systems (1994–2015). IEEE Transactions on Fuzzy Systems. 2017;26(2):430-42. [Google Scholar]
- Franceschet M. A comparison of bibliometric indicators for computer science scholars and journals on Web of Science and Google Scholar. Scientometrics. 2010;83(1):243-58. [Google Scholar]
- Setti G. Bibliometric indicators:Why do we need more than one?. IEEE Access. 2013;1:232-46. [Google Scholar]
- Thomaz PG, Assad RS, Moreira LF. Using the impact factor and H index to assess researchers and publications. Brazilian archives of cardiology. 2011;96:90-3. [Google Scholar]
- Halim Z, Khan S. A data science-based framework to categorize academic journals. Scientometrics. 2019;119(1):393-423. [Google Scholar]
- Aggarwal CC, Reddy CK. Data clustering. Algorithms and Applications. 2016 [Google Scholar]
- Jain AK. Data clustering:50 years beyond K-means. Pattern recognition letters. 2010;31(8):651-66. [Google Scholar]
- Roldan-Valadez E, Salazar-Ruiz SY, Ibarra-Contreras R, Rios C. Current concepts on bibliometrics:a brief review about impact factor, Eigenfactor score, CiteScore, SCImago Journal Rank, Source-Normalised Impact per Paper, H-index, and alternative metrics. Irish Journal of Medical Science (1971). 2019;188(3):939-51. [Google Scholar]
- Liu XZ, Fang H. A comparison among citation-based journal indicators and their relative changes with time. Journal of Informetrics. 2020;14(1):101007 [Google Scholar]
- Walters WH. Citation-based journal rankings:Key questions, metrics, and data sources. IEEE Access. 2017;5:22036-53. [Google Scholar]
- Ioannidis JP, Baas J, Klavans R, Boyack KW. A standardized citation metrics author database annotated for scientific field. PLoS Biology. 2019;17(8) [Google Scholar]
- Yan E, Wu C, Song M. The funding factor:A cross-disciplinary examination of the association between research funding and citation impact. Scientometrics. 2018;115(1):369-84. [Google Scholar]
- Zhao SX, Lou W, Tan AM, Yu S. Do funded papers attract more usage?. Scientometrics. 2018;115(1):153-68. [Google Scholar]
- Roshani S, Bagherylooieh MR, Mosleh M, Coccia M. What is the relationship between research funding and citation-based performance? A comparative analysis between critical disciplines. Scientometrics. 2021;126(9):7859-74. [Google Scholar]
- Haddawy P, Hassan SU, Asghar A, Amin S. A comprehensive examination of the relation of three citation-based journal metrics to expert judgment of journal quality. Journal of Informetrics. 2016;10(1):162-73. [Google Scholar]
- Maimon O, Rokach L. Decomposition methodology for knowledge discovery and data mining. InData mining and knowledge discovery handbook. 2005:981-1003. [Google Scholar]
- Kumar R, Rockett P. Multiobjective genetic algorithm partitioning for hierarchical learning of high-dimensional pattern spaces:a learning-follows-decomposition strategy. IEEE Transactions on Neural Networks. 1998;9(5):822-30. [Google Scholar]
- Dai J, Ren J, Du W. Decomposition-based Bayesian network structure learning algorithm using local topology information. Knowledge-Based Systems. 2020;195:105602 [Google Scholar]

