Contents
ABSTRACT
Research performance evaluation and ranking are crucial, as policymakers, funding institutions, administrators and researchers rely on these evaluations for resource allocation, strategic decision-making and policy formulation in research and innovation. Bibliometric data have been thoroughly used in measuring research performance and quality at the institutional level using publication and citation-related metrics. This study introduces a novel, multistage PCA-based composite index that integrates five aspects of cc namely publication, authorship, collaboration, sponsorship and impact or citation. These aspects represent input, process, output and outcome elements of a system. This data-driven approach provides a comprehensive benchmarking tool to rank countries’ research performance. As a use case, the composite index is used to compare the performance of blockchain research between countries based on a wide selection of bibliometric data prepared to accommodate the demographic variation among countries. The ranks obtained from the composite index perform better than the h-index in differentiating lower-ranked countries by incorporating collaboration, authorship and sponsorship parameters alongside publication and citation metrics, contributing to the index’s robustness. The implications of this study suggest that research performance evaluations should consider a wider set of factors to better reflect the complexities of national research ecosystems. Future policy decisions could be enhanced by adopting such comprehensive benchmarking tools, encouraging strategic decisions such as resource allocation, talent development and collaboration initiatives.
INTRODUCTION
The evaluation and ranking of research performance have become increasingly important in today’s academic environment, influencing the paths taken by academic institutions and nations worldwide. Policymakers, funding agencies, academic administrators and researchers all depend on the evaluation of research performance as a crucial instrument for resource allocation, strategic decision-making and the creation of research and innovation policies. Research performance rankings are important because they not only measure the contributions made by academic institutions but also have an impact on their financing opportunities, international partnerships and general standing in the academic community.[1,2]
Currently, there are issues concerning research performance measurement and ranking. One important issue is that the metrics tend to focus on production quantity and citation/impact aspects of research performance.[3] One popular research performance metric is the h-index, that combines both productivity and impact of research publication. However, using h-index in a measurement has limitations as it only takes into account the quantity of papers and citations as parameters, ignoring other factors like author contribution and collaboration.
The diversity in research ecosystems-where factors like collaboration patterns and funding sources vary significantly-necessitates a more nuanced approach. Therefore, a more comprehensive bibliometric based composite index is needed for research benchmarking which considers other aspects of research performance and applies specific weight for each aspect.
The importance of composite indices in research performance measurement lies in their ability to provide a more holistic view of research output than separate individual indicators. By combining multiple indicators into a single score, composite indices can capture the multidimensional nature of research performance and provide a more accurate representation of an entity’s overall research output.
Composite indices can be developed using various techniques and this research focuses on using a multivariate statistical technique called the Principal Component Analysis (PCA), which is a popular method for reducing the dimensionality of data.[6] A composite index based on PCA allows for the incorporation of multiple dimensions of research performance into a single, comprehensive metric.[7] PCA is particularly suited for this purpose as it reduces the dimensionality of the data while retaining the most critical information, ensuring that the index is not only inclusive but also robust in differentiating between countries with varying research capacities. This multidimensional approach is essential for policymakers and institutions seeking to make informed decisions based on a holistic understanding of research performance.
The objective of this research is to develop a multistage PCA-based composite index using bibliometric data to provide a comprehensive benchmarking tool for comparing research performance across nations. To accomplish the objective, we investigate (1) which bibliometric parameters can be used to calculate the composite index, (2) how this composite index for country research performance can be calculated using PCA and (3) how it is validated.
Our research attempts to employ all of the significant aspects that bibliographic data can provide, in addition to publications and citations related metrics. These aspects include publication, authorship, collaboration, sponsorship and impact or citation which represents input, process, output and outcome elements of a system.[8]
The proposed composite index is applied to rank the country’s performance of blockchain research as a case study. Blockchain, the underlying technology of prominent bitcoin cryptocurrency,[9] represents a rapidly emerging and highly interdisciplinary field with significant global relevance. As an area that intersects computer science, economics, law and various other domains, blockchain serves as an ideal example to test the robustness of the composite index. The field’s nascent stage means that countries are at different levels of development in their blockchain research efforts, providing a diverse dataset for comparison. Moreover, the innovative nature of blockchain technology, with its potential to revolutionize industries through decentralized and transparent systems[10,11] underscores the importance of accurately benchmarking research performance in this domain.
Among several studies on benchmarking blockchain research, one study by Wang, et al. specifically assesses the current state of blockchain research worldwide. However, this research compares many bibliometric parameters without using a composite index and focuses more on comparison of China’s and United States blockchain research and development stage. By applying the composite index to blockchain research, we demonstrate its capability to capture the multidimensional aspects of research performance across a cutting-edge and globally significant field.
The multistage PCA technique using five aspects of bibliometric data, namely publication, authorship, collaboration, sponsorship and impact or citation, offers a comprehensive data-driven approach in the development of research performance composite index.
This paper is organized as follows. In the literature review section several measurements and ranking systems are elaborated, as well as PCA techniques used in developing composite indexes. The following section explains the methodology to calculate multistage PCA-based composite index using bibliometric data. Then we show the results and present the analysis and discussion in the corresponding sections. Finally, we draw conclusions and recommend areas for future research.
LITERATURE STUDY
h-index is a metric initially designed to assess research performance of a scholar using bibliometric indicators of productivity and impact of research publication and is calculated as the h number of papers having at least h number of citations.[4] Originally used to measure performance of researchers on an individual level, it is expanded to measure research performance at institutional or even country level.[13,14] However, using H-index in a measurement has limitations as it only takes into account the quantity of papers and citations as parameters, ignoring other factors like author contribution and collaboration.[5]
Measurement of research performance and quality at the academic institutional level are mostly performed using Bibliometric data. Center for World University Ranking (CWUR), Leiden ranking, SCImago Institutions Rankings World Report and Shanghai Academic Ranking of World Universities (ARWU) are among many metric systems that use publication and citation-related metrics in their evaluation of research and academic quality around the world.[8] These rankings focus primarily on global universities, with the exception of the Leiden Ranking, which also accounts for research collaboration.[15] Notably, only SC Imago offers country-level rankings based on the number of scientific publications and citations.
Other measurements to rank national universities have also been proposed to use bibliometric data by taking into account the relative size of the institutions. One measurement calculates a bidimensional quantitative-qualitative index to compare the research output of a group of institutions in a given field.[16] Another one calculates composite indices specifically developed for the purpose of national comparison of universities in India, using quality and quantity indicators related to publication, citation and collaboration.[17,18] These measurements apply equal weight for all selected indicators to calculate their composite indices using geometric and algebraic mean respectively.
All research performance measurements described above use limited bibliometric indicators (mostly publication and citation-related) which are considered inadequate when applied to smaller size and globally unrecognized institutions.[19]
Composite indices are used to measure multidimensional phenomena in various domains, including to compare and rank country performance in areas such as industrial competitiveness, sustainable development, globalization and innovation.[20] On a country level, several composite indices have been developed to measure national research performance. A renowned Global Innovation Index uses research capacity and achievements such as number of patents or H-index in their measurement.[21] Another measurement method proposes using geometric mean of bibliometric indicators across different fields of research.[22] The latter also uses limited bibliometric data such as publications and citation and perform equal weighting in measuring the research performance at the country and institutional levels.
Among the numerous academic studies on country-level composite indices, one notable study suggests a multistage approach to calculate composite index, in this case for the seventh SDG goal to accommodate multidimensional phenomenon of energy sustainability. This approach helps in grouping a large number of variables in a hierarchical manner, thereby helping in simplifying the analysis of system behavior. Apart from using equal weightings, this research also uses the Analytic Hierarchy Process (AHP) to assign different weights to accommodate the influence of each dimension.[23]
Principal Component Analysis (PCA) is often used for developing composite indices, offering an effective method to aggregate complex information. PCA is a statistical technique to reduce the dimensionality of the data by transforming related variables into a set of uncorrelated principal components. This is done by identifying the most important components that explain the majority of variance in the data.[7] Given this characteristic, PCA is widely used for assigning weights in composite indices based on the variance contribution of the principal components.
By combining multistage approach and PCA as a data driven approach in assigning weights and calculating the composite index, a wider range of bibliometric data-beyond just publication and citation-related metrics, such as authorship, collaboration and sponsorship-can be utilized to more accurately reflect a country’s research performance.
Defining the conceptual framework
It is fundamental to be able to clearly describe the phenomenon being measured; in this case the research publication and performance, to help comprehend the big picture, communicate with others and facilitate further analysis.
Selection of parameters
Parameters that capture various aspects of research publication should be taken into account. The selection of each parameter is justified based on its relevance and significance in assessing the state of research publication in some constituents.
Data preparation and standardization
Data preparation involves data acquisition, cleansing and transformation to ensure suitability of acquired data to previously defined parameters, data relevance and quality as well as normal distribution of parameters. In addition, all parameters should be adequately comparable or standardized before being aggregated into a composite index using standardization method, to ensure their sensitivities to the composite index.
Calculation of correlation matrix
The correlation matrix shows correlation between a set of selected parameters. High correlation is preferable in PCA as it enables significant dimensional reduction where a few Principal Components (PCs) represent the dominant variance of the variables.
Weighting Methodology for the aggregation of individual parameters
The weighting methodology determines the relative importance or contribution of each parameter in the overall index. By using PCA as a data-driven approach, PCA loadings can be used as the weights for the aggregation.
Calculation of the composite index
The composite index is calculated in two stages. First, a few indicators are calculated as the weighted sum of their associated parameters. And in turn the composite index is calculated as the weighted sum of the indicators.
Validation
The composite index result is validated by comparing the country ranks based on the composite index values with the H-index rank.
Sensitivity Analysis
The sensitivity analysis is performed by excluding each of the five indicators to analyze the influence exerted by the excluded indicator.
Designing Conceptual Framework for Research Performance Composite Index
As shown in the Conceptual Framework Diagram in Figure 1, the research performance composite index is calculated using the combination of several bibliometric indicators. The aggregation to calculate the composite index is then performed in 2 (two) stages. In the first stage, the calculation of each indicator is done using their related parameters. In the second stage, five indicators from the first stage are used to calculate the composite index. A multivariate analysis technique called PCA is adopted in this multistage calculation of the composite index in order to reduce the dimensions while retaining most of the information and calculate both the indicators and index values.
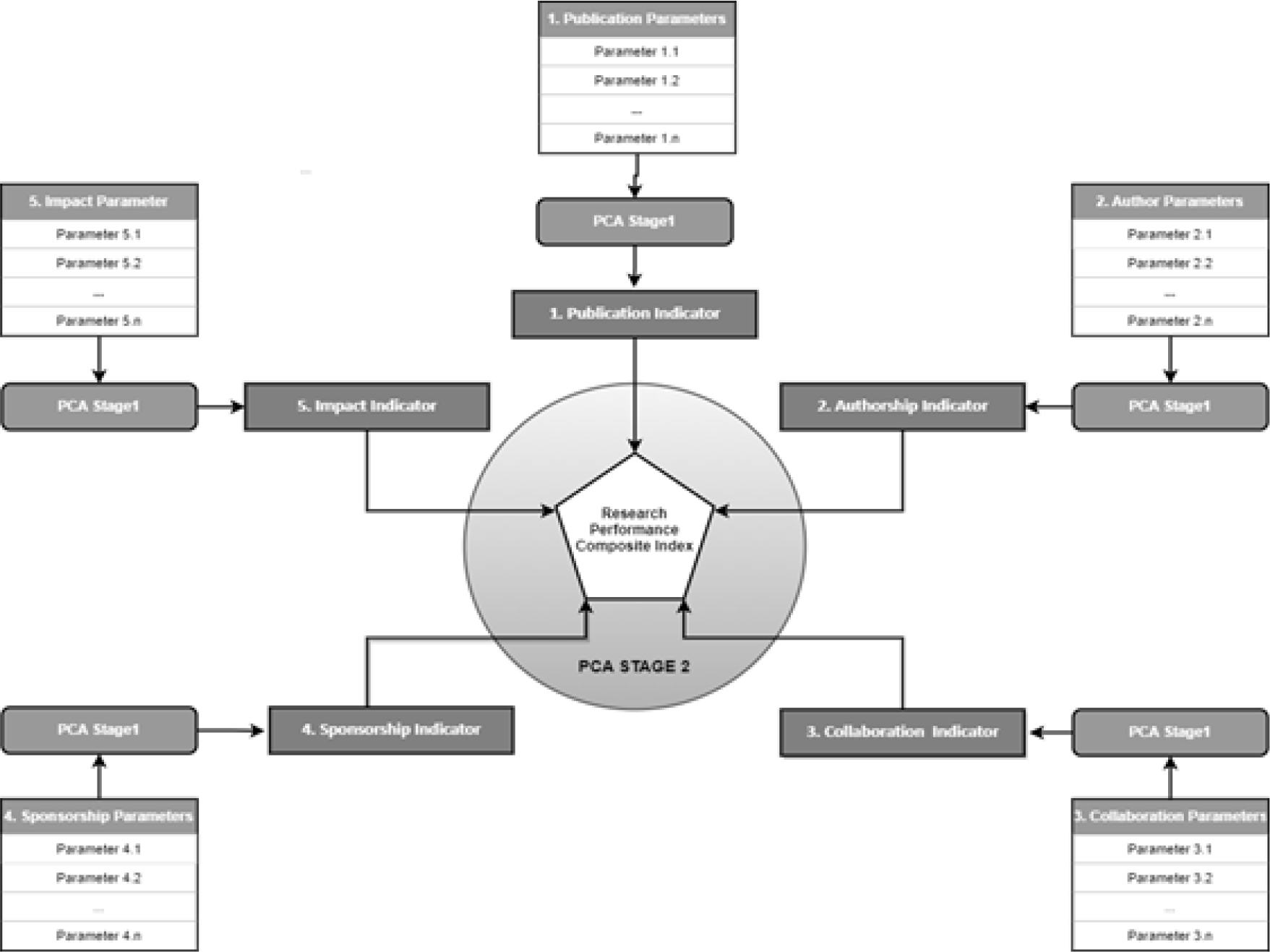
Figure 1:
The Conceptual Framework Diagram.
Bibliometric parameters which capture various aspects of the research domain can be grouped into several measurable performance indicators. These indicators try to capture the publication, citation and publication-citation related metrics.[25] For this composite index, we expand by emphasizing the importance of 5 (five) indicators, namely publication, authorship, collaboration, sponsorship and impact/citation aspects in the research publication performance. These indicators represent input, process, output and outcome elements of a system.[8] Authorship and sponsorship indicators characterize the input, collaboration the process, publication the output and citation the outcome of a research endeavor.
The 1st indicator describes the production aspect of research, which contains parameters related to publication output in the research domain. The 2nd indicator describes the authorship aspect of research publication through selected parameters related to authorship pattern and author collaboration. The authorship pattern parameters portray the leadership role in research and individual contribution to knowledge advancement in the research domain. Author collaboration reflected in team size and degree of collaboration, described further in the 3rd indicator portraying national or global collaboration. Research collaborations can lead to increased research productivity. With multiple researchers working together, tasks can be distributed more efficiently. This can result in faster data collection, analysis and publication of research findings, which can contribute to greater impact. The 4th indicator describes the sponsorship aspect of research that contains parameters that reflect the level of credibility of research to the stakeholders. This indicator is deemed important as publications from sponsored research, especially from research grants, indicate higher impacts in terms of journal ranking and citation counts than non-sponsored research. Lastly, the impact indicator describes research impact based on citation count, which portrays the influence of the research publication to another research.
Parameters Construction
A set of parameters are selected for each indicator that represent performance measures of their respective indicators. To accommodate the demographic variation among countries, the parameters are divided into quantity and quality parameters. Quantity parameters are size-dependent or extensive, i.e. larger countries are expected to have larger values of extensive parameters. Conversely, quality parameters are size independent or intensive, i.e. their values are not necessarily proportional to the country size.[18] In this research a number of size dependent parameters of total counts and size independent parameters of performance measures per total publication ratio are selected for each type of indicator.[29]
Data Preparation
The dataset in this research was acquired and processed using PRISMA methodology.[30] Initial 25415 bibliographic data was downloaded in October 2023 from the Web of Science Core Collection database, containing bibliographic data of journal articles, conference papers, book chapters and reviews with blockchain as topic (with search term: blockchain or “block-chain” or “block chain” or “distributed ledger technology”) that were published up until 2022. Further screening and eligibility testing, in which data unrelated to distributed ledger technology were excluded, resulted in 24516 publication data starting from 2013 until 2022.
For the country analysis, the dataset was processed according to the affiliation data, resulting in an expanded dataset of 36149, due to collaborative publications being attributed to each collaborating country. Based on this dataset, blockchain research publication data are summarized into 150 country data. Sponsorship information such as total sponsored paper and total sponsors can be extracted from funding agency information included in the acknowledgment paratext of scientific publications. This information can be used to analyze relationships between funding inputs and research outputs such as publications.[31] Some additional data is also added to this country dataset, to populate all of the quantity and quality parameters .
PCA is a type of multivariate analysis in which the original parameters are linearly combined to create each PC. In multivariate analysis normal distribution assumption of the parameters is necessary to yield a consistent result.[32] Detailed inspection into the frequency distribution/density of each parameter reveals that some of the parameters have skewed distributions as shown in the left column of Figure 2. Most quantity parameters and some quality parameters in all five indicators are highly skewed. To lessen skewness and approximate normality, the Yeo-Johnson power transformation is utilized in this research.[33]

Figure 2:
Density plot before and after Yeo-Johnson transformation.
R packages such as R core packages[34] including stats, corrr[35], ggplot2[36] and VGAM[37], as well as Microsoft Excel spreadsheets are used for the data processing and analysis.
Principal Component Analysis
PCA is a statistical technique used to reduce the dimensionality of the data and identify the most important components that explain the majority of the variation in the data. The goal of PCA is to explain most of the variability in a dataset with fewer variables than the original dataset. PCA is applied to the standardized data to identify the PCs that capture the underlying patterns and structure of the indicators. The eigenvalues and eigenvectors generated by PCA provide insights into the relative importance of each indicator.
PCA consists of 5 steps: data standardization, covariance/correlation matrix computation, determination of Eigen values and eigenvectors, selection of PCs, data transformation in new space.[38]
Standardization is done to eliminate the bias between parameters, which can happen if, for example, some parameters have larger ranges of values compared to others. Those parameters with larger ranges will dominate over those with small ranges and PCA is sensitive to the variances of the parameters. There are several methods to standardize data; one popular method adopted for this research is the z-score normalization method.[39] In this method each datum is subtracted by the mean and then divided by the standard deviation as shown by the formula below. As a result, the data is scaled to have a mean of 0 and a standard deviation of 1.
Correlation matrix is calculated to inspect the relationships between parameters which indicate redundancy. The correlation value and sign indicate the degree and direction of linear relationship between parameters respectively. High correlation between parameters indicates potential reduction of parameters in PCA.
Eigen values and eigenvectors of the correlation matrix are calculated using the following formula.
A: The correlation matrix,
v: The eigenvector,
λ: The eigenvalue.
Eigenvectors reflect the direction of the dominant variances in the data and are orthogonal to each other. Eigen values reflect the magnitude of these variances.
Each PC is a linear combination of the original parameters, where the coefficients are the eigenvector or the loadings corresponding to that particular PC. These loadings indicate the contribution of the original parameters to the PC. Due to this characteristic, PCA can be used as a data-driven approach to assign the weighting of each indicator[40], instead of relying solely on expert opinions or subjective judgments.
The percentage of total variance is a fundamental tool to assess the quality of the resulted low-dimensional representations of the dataset. Determining the number of PCs to keep is usually done by applying a predetermined percentage (70%) of the total variance as a cut-off point.
The PCA scores are the result of projecting the data onto each PC, so the scores are the value of data points along PCs. For each PC, the score is calculated as a weighted linear combination of standardized parameters’ values using the corresponding eigenvector’s loadings as the weight.
Yj: The score of sample j,
wij: The weight of paramater i of sample j,
xij: The value of parameter i of sample j,
p: The number of parameters.
Calculation of the composite index
If the first PC’s proportion of variance is larger than 70%, the PCA score of the first PC can be used as the composite index. Otherwise, it is calculated as the weighted sum of PCA scores using the proportion of variances as the weights.
CI: the composite index,
Wi: the proportion of variance of PCi,
Yi: the score of PCi,
p: the number of selected PCs.
In this research, the above formula is used to calculate indicator values in the first stage and the composite index in the second or final stage.
Validation
To validate the result, the countries’ ranks based on the composite index scores are compared to the ranks based on the country H-indices. H-index is widely used as a measure of research performance as it combines both productivity and impact of research publication. The validation is done by calculating the Spearman rank correlation coefficient between the 2 sets of rank using R.[34] The formula to calculate the coefficient is as follows.[41]
ρ: is the Spearman coefficient,
d: is the difference between 2 sets of item’s rank,
n: is the number of items.
Sensitivity Analysis
The objective of sensitivity analysis is to determine how changes of an independent variable affect a particular dependent variable.[42] The sensitivity analysis is performed by excluding each of the five indicators to analyze the influence exerted by the excluded indicator. This would result in five combinations of sensitivity analysis due to the existence of five indicators. For each combination, the Mean Absolute Rank Difference (MARD) is calculated using the formula:
N: number of countries,
Ranki, ref : rank of country i where all indicators are used to calculate the index.
Ranki,-p : rank of country i where indicator p is excluded.
The MARD value for each combination shows the effect of exclusion of one indicator to the average shift in ranks of countries. Thus, it measures the sensitivity of the composite index to the change in each indicator.
To quantify the overall effect on the variation of scores that a country experiences, the absolute difference between the reference score and the score obtained for a given combination of sensitivity analysis are calculated. The average of the absolute difference value obtained for the five combinations of analysis is considered as the average score variation of the country. To calculate the average effect of the 5 combinations to each country rank, we use the formula:
M: number of indicators,
Ranki, ref : rank of country i where all indicators are used to calculate the index.
Ranki,-p : rank of country i where indicator p is excluded.
This yields perspectives on the country’s research performance under various combinations.
RESULTS
Parameter Construction
A set of parameters have been selected for each indicator as shown in Table 1. These parameters represent performance measures of their respective indicators in accordance with the conceptual framework defined in Figure 1.
| Indicators | Parameters | |
|---|---|---|
| Quantity | Quality | |
| Publication | Total Journal Articles (papers) | Total Journal Articles Per TP (%) |
| Total Conference Papers (papers) | Total Conferences Paper Per TP (%) | |
| Total Reviews (papers) | Total Reviews Per TP (%) | |
| Total Book Chapters (papers) | Total Book Chapters PerTP (%) | |
| Authorship | Total Authors (author) | Total Authors Per TP (author/ paper) |
| Total Corresponding Authors (author) | Total Corresponding Authors Per TP (author/paper) | |
| Total Sole Authored Papers (paper) | Total Sole Authors PerTP (%) | |
| Total First Authored Papers (paper) | Total First Authored Papers PerTP (%) | |
| Collaboration | Total Collaborating Countries (countries) | Total Collaborating Country Per TP (countries/paper) |
| Total Affiliations (affiliation) | Total Affiliation Per TP (affiliation/paper) | |
| Total International Collaborating Papers (papers) | Total International Collaborating Paper Per TP (%) | |
| Sponsorship | Total Sponsored Papers (papers) | Total Sponsored Paper Per TP (%) |
| Total Sponsors (sponsors) | Total Sponsor Per TP (sponsors/paper) | |
| Total Papers Sponsored by Own Country (papers) | Total Sponsored by Own Country Per TP (%) | |
| Total Papers Sponsored by Other Country (papers) | Total Sponsored by Other Country Per TP (%) | |
| Impact | Total Citations (citations) | Total Citation Per TP (citations/paper) |
| Total Top 10% of Highly Cited Papers (papers) | Top 10% Per TP (%) | |
| Total Cited Publications | Total Cited Publications per TP (%) | |
Data Preparation and Standardization
Detailed inspection into the frequency distribution/density of each parameter reveals that some of the parameters have skewed distributions as shown in the left column of Figure 2. Most quantity parameters and some quality parameters in all five indicators are highly skewed. As shown in the right column of Figure 2, application of the Yeo-Johnson power transformation significantly reduces the skewness of most parameters.
The scale () function in R[34] is used to standardize the data of blockchain research publication parameters of 150 countries. As the dataset demonstrates that the parameters have varying ranges of value, this standardization results in each parameter scaled to have a mean of 0 and a standard deviation of 1.
Correlation of Indicator’s Parameters
To investigate the correlation between parameter pairs in each indicator, the cor() function[35] is used and visualized in Correlation Matrix Heat Maps (see Figure 3) using ggcorrplot() function.[36] It can be observed that the quantity or size-dependent parameters in each indicator have high or strong correlation with one another. On the other hand, the quality or size-independent parameters have varying levels of correlation with one another and relatively weak correlation with the quantity parameters. Highly correlated parameters potentially can be collapsed into one PC using PCA.

Figure 3:
The Correlation Matrices of the 5 Indicators.
Weighting and Aggregation (using PCA)
PCA is performed to determine the indicators in the first stage and composite index in the second stage. All the indicators and the composite index are calculated by applying princomp () function[34] to each dataset.
Indicators
Table 2 shows the PCs’ standard deviations, proportion of variances and cumulative proportions for each of the 5 (five) indicators. The indicators’ values are calculated as a weighted sum of the first n PCs’ scores using their respective proportions of variance as the weight, assuming the nth cumulative proportion of variance exceeds the 70% cut-off point requirement for PC selection. The data in Table 2 demonstrate that for publication indicator the cumulative proportion of the first three PCs surpasses 70%. Consequently, the publication indicator is calculated as the weighted sum of the first three PCs’ scores using the corresponding proportion of variances as the weights. On the other hand, for the remaining four indicators the cumulative proportion of the first two PCs already surpasses 70%. Consequently, the authorship, collaboration, sponsorship and impact indicators are calculated as the weighted sum of the first two PCs’ scores using the corresponding proportion of variances as the weights.
| Sl. No. | Indicator | Proportion of Variance | ||
|---|---|---|---|---|
| PC1 | PC2 | PC3 | ||
| 1 | Publication | |||
| Standard deviation | 1.872 | 1.286 | 1.185 | |
| Proportion of Variance | 0.438 | 0.207 | 0.175 | |
| Cumulative Proportion | 0.438 | 0.645 | 0.820 | |
| 2 | Authorship | |||
| Standard deviation | 2.073 | 1.420 | 0.880 | |
| Proportion of Variance | 0.537 | 0.253 | 0.097 | |
| Cumulative Proportion | 0.537 | 0.789 | 0.886 | |
| 3 | Collaboration | |||
| Standard deviation | 1.759 | 1.560 | 0.612 | |
| Proportion of Variance | 0.516 | 0.405 | 0.062 | |
| Cumulative Proportion | 0.516 | 0.921 | 0.983 | |
| 4 | Sponsorship | |||
| Standard deviation | 2.235 | 1.156 | 0.965 | |
| Proportion of Variance | 0.624 | 0.167 | 0.116 | |
| Cumulative Proportion | 0.624 | 0.791 | 0.908 | |
| 5 | Impact | |||
| Standard deviation | 1.894 | 1.066 | 0.950 | |
| Proportion of Variance | 0.598 | 0.189 | 0.151 | |
| Cumulative Proportion | 0.598 | 0.787 | 0.938 | |
Component loadings of each indicator show the importance of their respective parameters to a particular PC. As shown in Table 3, for all indicators, all quantity parameters mainly contribute to the first component (PC1), whereas most of the quality parameters contribute to the second or third components. For example, for the first indicator, total articles, total conference papers, total reviews and total book chapters have high loadings on PC1, whereas the remaining parameters have high loadings on PC2 and PC3. For the second indicator, total authors, total corresponding authors, total first authored papers and total sole authored paper have high loadings on PC1, whereas the remaining parameters have high loadings on PC2. Similarly for collaboration, sponsorship and impact indicators the quantity parameters have high loadings on PC1, whereas most of the quality parameters have high loadings on PC 2. Since PC1 has the highest proportion of variance for each indicator (44%, 54%, 52%, 62% and 60% respectively), the quantity parameters have a dominant contribution to the calculation of indicators’ values.
| Publication | PC1 | PC2 | PC3 | Sponsorship | PC1 | PC2 |
|---|---|---|---|---|---|---|
| TotalArticle | 0.52 | 0.12 | 0.03 | TotSponsoredPapers | 0.41 | 0.28 |
| TotalConfPaper | 0.52 | -0.11 | 0.07 | TotSponsors | 0.42 | 0.23 |
| TotalReview | 0.50 | 0.05 | -0.17 | TotSponsoredByOwnCountry | 0.38 | 0.33 |
| TotalBookChapter | 0.44 | -0.06 | -0.19 | TotSponsoredByOtherCountry | 0.40 | 0.25 |
| TotArticlePerTP | 0.07 | 0.72 | 0.29 | TotSponsoredPapersPerTP | 0.35 | -0.46 |
| TotConfPaperPerTP | 0.09 | -0.66 | 0.42 | TotSponsorPerTP | 0.36 | -0.39 |
| TotReviewPerTP | -0.08 | -0.01 | -0.66 | TotSponsoredbyOwnCountryPerTP | 0.24 | -0.09 |
| TotBookChapterPerTP | -0.03 | -0.13 | -0.49 | TotponsoredByOtherCountryPerTP | 0.21 | -0.56 |
| Authorship | PC1 | PC2 | Impact | PC1 | PC2 | |
| TotalAuthors | 0.44 | 0.24 | TotalCitation | 0.51 | 0.19 | |
| TotCorresAuthors | 0.47 | 0.11 | TotHaveCitation | 0.48 | 0.35 | |
| TotFirst.AuthoredPapers | 0.47 | 0.11 | Top10 | 0.48 | 0.22 | |
| TotalSoleAuthoredPapers | 0.44 | 0.05 | TotCitationPerTP | 0.42 | -0.36 | |
| TotalAuthorPerTP | -0.05 | 0.61 | TotHaveCitationPerTP | 0.27 | -0.46 | |
| TotCorresAuthPerTP | 0.25 | -0.38 | Top10PerTP | 0.13 | -0.68 | |
| TotFirstAuthoredPaperPerTP | 0.31 | -0.27 | ||||
| TotSoleAuthorPerTP | 0.04 | -0.57 | ||||
| Collaboration | PC1 | PC2 | ||||
| TotalCollabCountries | 0.55 | 0.18 | ||||
| TotalAffiliations | 0.54 | 0.19 | ||||
| TotIntCollabPapers | 0.54 | 0.18 | ||||
| TotalCollabCountryPerTP | -0.21 | 0.57 | ||||
| TotAffiliationPerTP | -0.11 | 0.59 | ||||
| TotIntCollabPapersPerTP | -0.25 | 0.48 |
Composite Index
In step 2, the 5 (five) indicators’ values are used as the parameters to generate the composite index using the PCA technique. The density plot and correlation matrix in Figure 4 demonstrates the density of each parameter and correlations between pairs of parameters. It can be observed that skewness of each parameter is low and the correlations among all 5 (five) parameters are strong, which implies the suitability of PCA to calculate the composite index since PCs are linear combinations of the scaled original parameters.

Figure 4:
The density Plot and Correlation Matrix of Indicators.
The PCs’ proportion of variance in Figure 5 shows that the first PC (PC1) represents 90.5% of cumulative variance, which exceeds the 70% cut-off point requirement for PC selection. Consequently, the PC1’s score can be directly used as the Composite Index.

Figure 5:
Proportion of Variance Composite Index.
As shown in Table 4 all five indicators have comparable loadings to the first component (PC1). It can be inferred that authorship, collaboration and sponsorship indicators contribute almost equally to the composite index as publication and impact indicators.
| Indicator | PC1 |
|---|---|
| Publication | 0.441 |
| Authorship | 0.454 |
| Collaboration | 0.442 |
| Sponsorship | 0.444 |
| Impact | 0.455 |
Table 5 shows the Indicators, Composite Index, H index, Composite Index rank and H index rank for the top 10 countries.
| Country | Indicator | CI | CI rank | H index | H index rank | ||||
|---|---|---|---|---|---|---|---|---|---|
| Publication | Authorship | Collaboration | Sponsorship | Impact | |||||
| CHINA | 2.343 | 3.256 | 2.258 | 4.573 | 2.676 | 5.83 | 1 | 148 | 1 |
| USA | 2.210 | 2.744 | 2.171 | 2.690 | 2.602 | 4.91 | 2 | 147 | 2 |
| ENGLAND | 1.932 | 2.115 | 2.053 | 1.888 | 2.165 | 4.06 | 4 | 96 | 3 |
| INDIA | 2.127 | 2.461 | 1.816 | 2.107 | 2.084 | 4.23 | 3 | 86 | 5 |
| AUSTRALIA | 1.707 | 2.055 | 1.877 | 2.288 | 2.085 | 3.94 | 5 | 92 | 4 |
| CANADA | 1.543 | 1.872 | 1.718 | 2.756 | 1.960 | 3.83 | 6 | 81 | 6 |
| SOUTH KOREA | 1.590 | 2.056 | 1.383 | 2.515 | 1.874 | 3.68 | 7 | 68 | 7 |
| GERMANY | 1.366 | 2.015 | 1.294 | 1.843 | 1.776 | 3.26 | 10 | 62 | 8 |
| ITALY | 1.491 | 2.097 | 1.408 | 1.549 | 1.759 | 3.30 | 9 | 61 | 9 |
| SINGAPORE | 1.054 | 1.424 | 1.435 | 2.977 | 1.676 | 3.25 | 11 | 58 | 12 |
ANALYSIS AND DISCUSSION
The result of the multistage PCA-based composite index calculation in Table 5 shows that China is the leader in blockchain research, followed by the USA, India, England and Australia. This is consistent with research discovery by Wang, et al. which demonstrates that China is the leader in blockchain research.[12]
Validation
To validate the result, the countries’ composite indices’ ranks are compared to their H-indices’ ranks by calculating the Spearman rank correlation coefficient between the 2 sets of rank using R.[34] The correlation is calculated and plotted as shown in Figure 5 using ggscatter() function.[36] It is found that the Spearman rank correlation coefficient is 0.97 and the corresponding p-value is less than 2,2e-16. Since the p-value is less than 0.05, the correlation is statistically significant.[43] This high coefficient value proves that there is a strong correlation between the 2 sets of rank, which means that the PCA-based Composite Index is validated as the measurement tool to determine leadership in research performance among countries. Figure 6 also demonstrates that the rank correlation is consistent across all countries with a few exceptions especially for lower rank countries. Figure 7 compares the relationship between the proposed Composite Index and the country H-index with countries ranks. It can be inferred that the relationship between Composite Indices and the ranks is quite linear for the entire range of ranks. Conversely, the relationship between H-indices and the ranks levels off beginning at the mid ranks down to the lower ranks. It can be concluded that the PCA-based composite index consistently provides better rank discrimination than country H-index.

Figure 6:
Spearman rank correlation.

Figure 7:
Comparison between the Composite Index and H-index.
Sensitivity Analysis
The Mean Absolute Rank Difference (MARD) for exclusion of each indicator shown in Figure 8 reveals the relative sensitivity of the composite index to each indicator. It can be inferred that the index is relatively more sensitive to Sponsorship (MARD=2.87) and Collaboration (MARD=2.67) consecutively.

Figure 8:
MARD value for exclusion of each indicator.
The availability of funding from sponsors is essential to a research project’s success since it affects the publishing of the paper, the researchers’ communication, accommodations and access to the required data. Publications from sponsored research, particularly from research funds, show larger impacts in terms of journal ranking and citation counts than non-sponsored research, which is why this indicator is considered significant.[28]
Collaboration is a crucial factor in research performance. It fosters knowledge sharing, resource pooling and the development of more impactful studies. Research collaborations can lead to increased research productivity.[26] When researchers from different institutions or countries collaborate, they can combine their expertise to achieve groundbreaking results. This can increase a country’s global visibility, improve resource access and influence policy decisions. As a result, the high sensitivity of a country’s research performance index to the collaboration indicator underscores the importance of collaboration in driving innovation and scientific advancement.
The average variations involved in each country’s ranking is depicted in Figure 9. The exclusion of indicators resulted in a maximum average rank variation of 10.4 corresponding to Cote d’Ivoire. However, the average rank variation for all 150 countries is only 2.5. Therefore, it shows robustness of the composite index as it is not overly sensitive to variation of indicators.

Figure 9:
Country’s MARD value.
Average rank variations of Panama and Mauritius are 8.2 and 7.2 mainly due to exclusion of sponsorship and collaboration indicators. This is consistent with our previous findings that the index is relatively more sensitive to Sponsorship and Collaboration.
Future Research
As a limitation, this research only utilizes bibliometric data related to scientific publication and does not utilize other data such as patents, amount of research grants, national demographic data, etc. Another limitation is that this research only uses the Web of Science database. Therefore, for future studies other bibliometric data sources such as Scopus and Dimensions, as well as non-bibliometric data can be included to get a more holistic view of country research performance.
Using PCA to calculate a composite index has several limitations that can impact the accuracy and interpretability of the results. One key limitation is that PCA assumes linearity, which may overlook complex, non-linear relationships between variables. Additionally, PCA is sensitive to outliers, which can skew the principal components and lead to a distorted composite index.[6]
Alternative approaches such as Partial Least Squares based Structural Equation Modeling (PLS-SEM)[44] and Robust PCA[45] can be employed to overcome the PCA limitation in handling non-linearity between variables and sensitivity to outliers.
Our research provides a foundation for advancing country-level benchmarking by offering a systematic and data-driven methodology for constructing composite indices. Future research can build on this framework to address the identified limitations and enhance the accuracy of the benchmarking process.
CONCLUSION
The proposed composite index provides a comprehensive benchmarking tool to compare country research performance based on bibliometric data using input-process-output-outcome system view. This research contributes to the bibliometric analysis literature by introducing a multistage PCA-based composite index that integrates diverse aspects of research performance beyond traditional publication and citation metrics. The inclusion of authorship, collaboration and sponsorship parameters offers a more comprehensive evaluation framework, improving the accuracy of country-level comparisons.
The aggregation to calculate the composite index is performed in 2 (two) stages. In stage one, the 5 (five) indicators are calculated using the combination of selected bibliometric parameters. In stage two, the composite index is calculated using the combination of the 5 indicators. The weighting factors for the bibliometric parameters and for the respective performance indicators are derived solely using PCA calculation. The relatively equal weighting between the five indicators as a result of the PCA emphasizes the significance of authorship, collaboration and sponsorship in calculating research performance.
Result validation is done by calculating the Spearman rank correlation coefficient between the Composite Indices’ ranks and the corresponding H-indices’ ranks. The high Spearman coefficient value proves that there is a strong correlation between the 2 (two) sets of ranks. Consequently, it can be concluded that the PCA-based Composite Index is suitable as the measurement tool to rank research performance among countries. This research also indicates the PCA-based composite index performs better than H-index in differentiating lower rank countries due to the adoption of collaboration, authorship and sponsorship related parameters as additions to the publication and citation related parameters.
The sensitivity analysis shows the composite index is most sensitive to Sponsorship and Collaboration, highlighting their importance in research success and productivity. Despite some larger rank changes for certain countries, the overall average rank variation of 2.5 demonstrates the index’s robustness to changes in indicators.
The multistage PCA-based composite index provides a valuable tool for policymakers and research institutions to benchmark research performance, helping to guide strategic decisions such as resource allocation, talent development and collaboration initiatives. By identifying strengths and weaknesses in research performance aspects, this index can support targeted interventions to improve research production and impact.
As limitations, only bibliometric data from the Web of Science database is used in this study. Future studies should incorporate broader data sources such as Scopus and Dimensions, as well as non-bibliometric data to get a more holistic view of country research performance. Furthermore, alternative approaches like PLS-SEM and Robust PCA can be employed to overcome the PCA limitation in handling non-linearity between variables.
Cite this article:
Kurniawan RD, Riza H, Wardhani SSW, Ba’Abdullah F, Kusumaningrum D. Advancing Country-Level Research Benchmarking: A Bibliometric Multistage Principal Component Analysis- Based Composite Index Approach. J Scientometric Res. 2025;14(1):16-31.
ACKNOWLEDGMENT
This research was conducted at the Research Center for Artificial Intelligence and Cyber Security, National Research and Innovation Agency (BRIN), Indonesia. No specific grant from any public, commercial, or non-profit funding agency was offered for the conduct of this research.
ABBREVIATION
| AHP | Analytic Hierarchy Process |
|---|---|
| ARWU | Academic Ranking of World Universities |
| CI | Composite Index |
| CWUR | Center for World University Ranking |
| MARD | Mean Absolute Rank Difference |
| PC | Principal Component |
| PCA | Principal Component Analysis |
| PLS-SEM | Partial Least Squares Structural Equation Modeling |
| PRISMA | Preferred Reporting Items for Systematic reviews and Meta-Analyses |
| SDGs | Sustainable Development Goals |
| VGAM | Vector Generalized Linear and Additive Models. |
References
- Hamann J. The visible hand of research performance assessment. High Educ.. 2016;72(6):761-79. [CrossRef] | [Google Scholar]
- Ianoş I, Petrişor AI. An overview of the dynamics of relative research performance in Central-Eastern Europe using a ranking-based analysis derived from SCImago data. Publications.. 2020;8(3):36 [CrossRef] | [Google Scholar]
- Fisher NI. Performance measurement: issues, approaches and opportunities. Harv Data Sci Rev.. 2021;3(4) [CrossRef] | [Google Scholar]
- Hirsch JE. An index to quantify an individual’s scientific research output. Proc Natl Acad Sci U S A.. 2005;102(46):16569-72. [PubMed] | [CrossRef] | [Google Scholar]
- Ding J, Liu C, Kandonga GA. Exploring the limitations of the h-index and h-type indexes in measuring the research performance of authors. Scientometrics.. 2020;122(3):1303-22. [CrossRef] | [Google Scholar]
- Jolliffe IT, Cadima J. Principal component analysis: a review and recent developments. Philos Trans A Math Phys Eng Sci.. 2016;374(2065):20150202 [PubMed] | [CrossRef] | [Google Scholar]
- Mazziotta M, Pareto A. On the construction of composite indices by principal components analysis. Riv Ital Econ Demogr Stat.. 2016:1 [PubMed] | [CrossRef] | [Google Scholar]
- Hermanu AI, Sondari MC, Dimyati M, Sari D. Study on university research performance based on systems theory: systematic literature review. Int J Prod Qual Manag.. 2022;35(4):447-72. [CrossRef] | [Google Scholar]
- Bitcoin NS. A peer-to-peer electronic cash system; 2008.
- Berryhill J, Bourgery T, Hanson A. Blockchains unchained: blockchain technology and its use in the public sector; 2018.
- Sanka AI, Irfan M, Huang I, Cheung RC. A survey of breakthrough in blockchain technology: adoptions, applications, challenges and future research. Comput Commun.. 2021;169:179-201. [CrossRef] | [Google Scholar]
- Wang Q, Su M, Li R. Is China the world’s blockchain leader? Evidence, evolution and outlook of China’s blockchain research. J Cleaner Prod.. 2020;264:121742 [CrossRef] | [Google Scholar]
- Csajbók E, Berhidi A, Vasas L, Schubert A. Hirsch-index for countries based on Essential Science Indicators data. Scientometrics.. 2007;73(1):91-117. [CrossRef] | [Google Scholar]
- Huang MH. Exploring the h‐index at the institutional level: A practical application in world university rankings. Online Inf Rev.. 2012;36(4):534-47. [CrossRef] | [Google Scholar]
- Vernon MM, Balas EA, Momani S. Are university rankings useful to improve research? A systematic review. PLOS ONE.. 2018;13(3):0193762 [PubMed] | [CrossRef] | [Google Scholar]
- Torres-Salinas D, Moreno-Torres JG, Delgado-López-Cózar E, Herrera F. A methodology for Institution-Field ranking based on a bidimensional analysis: the IFQ 2 A index. Scientometrics.. 2011;88(3):771-86. [CrossRef] | [Google Scholar]
- Uddin A, Singh VK. A quantity–quality composite ranking of Indian institutions in CS research. IETE Tech Rev.. 2015;32(4):273-83. [CrossRef] | [Google Scholar]
- Basu A, Banshal SK, Singhal K, Singh VK. Designing a Composite Index for research performance evaluation at the national or regional level: ranking Central Universities in India. Scientometrics.. 2016;107(3):1171-93. [CrossRef] | [Google Scholar]
- Sypsa V, Hatzakis A. Assessing the impact of biomedical research in academic institutions of disparate sizes. BMC Med Res Methodol.. 2009;9(1):33 [PubMed] | [CrossRef] | [Google Scholar]
- . OECD. 2008 Handbook on constructing composite indicators: methodology and user guide.
- World Intellectual Property Organization.. Conceptual Framework (Appendix 1). 2020 Global innovation index 2020: who will finance innovation?.
- Docampo D, Bessoule JJ. A new approach to the analysis and evaluation of the research output of countries and institutions. Scientometrics.. 2019;119(2):1207-25. [CrossRef] | [Google Scholar]
- Madurai Elavarasan R, Pugazhendhi R, Irfan M, Mihet-Popa L, Campana PE, Khan IA, et al. A novel Sustainable Development Goal 7 composite index as the paradigm for energy sustainability assessment: A case study from Europe. Appl Energy.. 2022;307:118173 [CrossRef] | [Google Scholar]
- Mazziotta M, Pareto A. On a generalized non-compensatory composite index for measuring socio-economic phenomena. Soc Indic Res.. 2016;127(3):983-1003. [CrossRef] | [Google Scholar]
- Donthu N, Kumar S, Mukherjee D, Pandey N, Lim WM. How to conduct a bibliometric analysis: an overview and guidelines. J Bus Res.. 2021;133:285-96. [CrossRef] | [Google Scholar]
- Tang C, Zhang G, Naumann SE. Do central country authors of international co-authored publication networks obtain a high research impact?. MJLIS.. 2017;22(3):1-17. [CrossRef] | [Google Scholar]
- Dusdal J, Powell JJ. Benefits, motivations and challenges of international Collaborative Research: A sociology of science case study. Sci Public Policy.. 2021;48(2):235-45. [CrossRef] | [Google Scholar]
- Wang J, Shapira P. Is there a relationship between research sponsorship and publication impact? An analysis of funding acknowledgments in nanotechnology papers. PLOS ONE.. 2015;10(2):0117727 [PubMed] | [CrossRef] | [Google Scholar]
- Costas R, Zahedi Z, Wouters P. The thematic orientation of publications mentioned on social media: large-scale disciplinary comparison of social media metrics with citations. Aslib J Info Mgmt.. 2015;67(3):260-88. [CrossRef] | [Google Scholar]
- Page MJ, McKenzie JE, Bossuyt PM, Boutron I, Hoffmann TC, Mulrow CD, et al. The PRISMA 2020 statement: an updated guideline for reporting systematic reviews. Int J Surg.. 2021;88:105906 [PubMed] | [CrossRef] | [Google Scholar]
- Grassano N, Rotolo D, Hutton J, Lang F, Hopkins MM. Funding data from publication acknowledgements: coverage, uses and limitations. SSRN Journal.. 2016 [CrossRef] | [Google Scholar]
- Hair JF, Hult GT, Ringle CM, Sarstedt M. A primer on partial least squares structural equation modeling (PLS-SEM).. 2017 [CrossRef] | [Google Scholar]
- Yeo IK. A new family of power transformations to improve normality or symmetry. Biometrika.. 2000;87(4):954-9. [CrossRef] | [Google Scholar]
- R Core Team.. 2023 R: A Language and Environment for Statistical Computing;.
- Kuhn M, Jackson S. 2022 corrr: correlations in R;.
- Kassambara A, Patil I. Ggcorrplot: visualization of a correlation matrix using ggplot2; 2023.
- . Vector generalized linear and additive models. 2024
- Jackson JE. A user’s guide to principal components.. 1991 [CrossRef] | [Google Scholar]
- Nisbet R, Miner G, Yale K, Elder JF, Peterson AF. Handbook of statistical analysis and data mining applications.. 2018 [CrossRef] | [Google Scholar]
- Chao YS, Wu CJ. Principal component-based weighted indices and a framework to evaluate indices: results from the Medical Expenditure Panel survey 1996 to 2011. PLOS ONE.. 2017;12(9):0183997 [PubMed] | [CrossRef] | [Google Scholar]
- McAleer P. A handy workbook for research methods & statistics;. 2021 [CrossRef] | [Google Scholar]
- Nayyeri M, Hosseini SA. Sensitivity analysis to determine the importance of input variables in groundwater stress. Phys Chem Earth Parts A B C.. 2024;135:103628 [CrossRef] | [Google Scholar]
- Sedgwick P. Spearman’s rank correlation coefficient. BMJ.. 2014;349:g7327 [PubMed] | [CrossRef] | [Google Scholar]
- Hair JF, Black WC., Babin BJ, anderson RE. Multivariate Data Anal (Eight Ed). 2019 [PubMed] | [CrossRef] | [Google Scholar]
- Candès EJ, Li X, Ma Y, Wright J. Robust principal component analysis?. J ACM.. 2011;58(3):1-37. [CrossRef] | [Google Scholar]

